Cette MiniRécup porte sur la résolution de problèmes liés aux fonctions abordées en 4e et en 5e secondaire. Tu trouveras aussi un résumé pour chaque fonction et un exercice récapitulatif qui te permettront de faire une courte révision à ce sujet.
Les problèmes abordés dans cette MiniRécup sont en lien avec les fonctions suivantes : la fonction polynomiale de degré 2, la fonction partie entière, la fonction racine carrée, la fonction valeur absolue, la fonction rationnelle, la fonction exponentielle et la fonction logarithmique.
Pour toutes ces fonctions, tu dois être capable de tracer le graphique et de trouver la règle. Tu dois aussi être en mesure de résoudre chacun de ces types d’équations.
Fonction polynomiale de degré 2 centrée à l’origine
||f(x)=ax^2||
Fonction polynomiale de degré 2 avec |a,| |h| et |k|
||f(x)=a(x-h)^2+k|| où |(h,k)| correspond aux coordonnées du sommet
Voici deux exemples de résolution d'équation polynomiale de degré 2 sous la forme canonique.
Soit la fonction |f(x)=3(x+7)^2-5.|
-
Détermine la ou les valeur(s) de |x| lorsque |f(x)=7.|||\begin{align} f(x) &= 3(x+7)^2 -5 \\ 7 &= 3(x+7)^2 -5 \\ \color{#ec0000}{\sqrt{\color{black}{4}}} &= \color{#ec0000}{\sqrt{\color{black}{(x+7)^2}}} \\ \pm\ 2 &= x+7 \\ -2 = x+7& \qquad\ \ \ \ \, 2 = x+7 \\ -9 = x_1\ \ \ \ \ &\qquad -5 = x_2 \end{align}||
-
Détermine la ou les valeur(s) de |x| lorsque |f(x)=-8.|||\begin{align}f(x)&=3(x+7)^2-5\\ -8&=3(x+7)^2-5\\-1&=(x+7)^2\quad \Rightarrow \text{impossible}\end{align}||Comme le nombre à gauche de l’équation n’est pas un nombre positif, on arrête la résolution. Il n’y a aucune solution lorsque |f(x)=-8.|
Si l’équation est plutôt donnée sous la forme générale, on met l’équation sous la forme |ax^2+bx+c=0| et on utilise la formule quadratique.
Fonction partie entière centrée à l’origine
||f(x) = a[bx]||
Fonction partie entière avec |a,| |b,| |h| et |k|
||f(x) = a[b(x-h)]+k||où |(h,k)| correspond aux coordonnées d’un point fermé
Voici deux exemples de résolution d'équation partie entière.
Soit la fonction |f(x)=-2[8(x-3)]+1.|
-
Détermine les valeurs de |x| lorsque |f(x)=2.|
||\begin{align}f(x)&=-2[8(x-3)]+1\\ 2&=-2[8(x-3)]+1\\-\dfrac{1}{2}&=[8(x-3)]\quad \Rightarrow \text{impossible}\end{align}||Comme la partie entière n’est pas un nombre entier, on arrête la résolution. Il n’y a aucune solution lorsque |f(x)=2.| -
Détermine les valeurs de |x| lorsque |f(x)=-5.|
||\begin{align}f(x)&=-2[8(x-3)]+1\\ -5&=-2[8(x-3)]+1\\3&=[8(x-3)]\end{align}||||\begin{align} 3\leq 8(&x-3) < 3+1 \\ \dfrac{3}{8}\leq\ &x-3 < \dfrac{4}{8} \\ \dfrac{3}{8} + 3\leq \ &x\ < \dfrac{1}{2} +3 \\ \dfrac{27}{8}\leq \ & x \ < \dfrac{7}{2} \\\\ x \in\ &\left[\dfrac{27}{8},\dfrac{7}{2}\right[ \end{align}||
Fonction racine carrée centrée à l’origine
||\begin{align} f(x) &= a\sqrt{b x} \\ &\text{ou} \\ f(x) &= a\sqrt{\pm x} \end{align}||
Fonction racine carrée avec |a,| |b,| |h| et |k|
||\begin{align} f(x) &= a\sqrt{b (x-h)}+k \\ &\text{ou} \\ f(x) &= a\sqrt{\pm (x-h)}+k \end{align}||où |(h,k)| correspond aux coordonnées du sommet.
Il faut tenir compte de deux restrictions particulières :
-
La racine carrée est toujours supérieure ou égale à |0.|
-
Le terme sous la racine carrée, appelé radicande, est toujours supérieur ou égal à |0.|
Voici deux exemples de résolution d'équation racine carrée.
Soit la fonction |f(x)=-7\sqrt{-(x+1)}+4.|
-
Détermine la valeur de |x| lorsque |f(x)=-2.| ||\begin{align} f(x) &= -7\sqrt{-(x+1)}+4 \\ -2 &= -7\sqrt{-(x+1)} + 4 \\ \left(\dfrac{6}{7}\right)^{\color{#ec0000}{2}} &= \sqrt{-(x+1)}^{\color{#ec0000}{2}} \\ \dfrac{36}{49} &= -(x+1) \\ -\dfrac{36}{49} &= x+1 \\ -\dfrac{85}{49} &= x \end{align}||
-
Détermine la valeur de |x| lorsque |f(x)=6.| ||\begin{align} f(x) &= -7\sqrt{-(x+1)} +4 \\ 6 &= -7\sqrt{-(x+1)} +4 \\ -\dfrac{2}{7} &= \sqrt{-(x+1)} \quad \Rightarrow \text{impossible} \end{align}||Comme la racine carrée est égale à un nombre négatif, on arrête la résolution. Il n’y a aucune solution lorsque |f(x)=6.|
Fonction valeur absolue avec |a|, |h| et |k|
||f(x)=a\vert x-h\vert+k|| où |(h,k)| correspond aux coordonnées du sommet
Lorsqu’une valeur absolue est isolée d’un côté de l’égalité, l’expression algébrique ou le nombre de l’autre côté doit être positif.||\vert x\vert=\underbrace{\dots}_{\ge\ 0}||
Voici deux exemples de résolution d'équation valeur absolue.
Soit la fonction |f(x)=-0{,}6\vert x-3\vert -1.|
-
Détermine la ou les valeur(s) de |x| lorsque |f(x)=-10.|||\begin{align}f(x)&=-0{,}6\vert x-3\vert -1\\-10&=-0{,}6\vert x-3\vert -1\\15&=\vert x-3|\end{align}||||\begin{align} 15&=x-3 &&-15=x-3\\18&=x_1 &&-12=x_2\end{align}||Les valeurs de |x| sont |-12| et |18.|
-
Détermine la ou les valeur(s) de |x| lorsque |f(x)=5.| ||\begin{align}f(x)&=-0{,}6\vert x-3\vert -1\\5&=-0{,}6\vert x-3\vert -1\\6&=-0{,}6\vert x-3\vert\\-10&=\vert x-3\vert \quad \Rightarrow\quad \text{impossible}\end{align}||Comme la valeur absolue est égale à un nombre négatif, on arrête la résolution. Il n’y a aucune solution lorsque |f(x)=5.|
Il y a deux façons d’écrire la règle d’une fonction rationnelle.
La forme canonique
||f(x)=\dfrac{a}{b(x-h)}+k||où
|x=h| est l’équation de l’asymptote verticale.
|y=k| est l’équation de l’asymptote horizontale.
Remarque : La plupart du temps, on utilise la forme canonique simplifiée. ||f(x)=\dfrac{a}{x-h}+k||
La forme générale
||f(x)=\dfrac{a_1x+b_1}{a_2x+b_2}||
Dans certains problèmes, il faut être capable de passer d’une forme à l’autre.
Pour passer de la forme canonique à générale, il faut écrire les 2 termes sur le même dénominateur et additionner les numérateurs.
Exemple :||\begin{align} f(x) &= \dfrac{5}{x-3}+4 \\&= \dfrac{5}{x-3}+ \dfrac{4\color{#ec0000}{(x-3)}}{1\color{#ec0000}{(x-3)}} \\&= \dfrac{5}{x-3}+ \dfrac{4x-12}{x-3} \\&= \dfrac{5+4x-12}{x-3} \\&= \dfrac{4x-7}{x-3} \\ \end{align}||Pour passer de la forme générale à la forme canonique, il faut effectuer la division entre le numérateur et le dénominateur.
Exemple :||\begin{align} f(x) &= \dfrac{8x-15}{2x-6} \\\\8x-15\ \ \, &\vert\! \underline{\ \ \color{#3B87CD}{2x-6}\ } \\\ \underline{-(8x-24)}\ &\quad \color{#3A9A38}{4} \\ \color{#FA7921}{9}\ \,\, \\\\f(x) &= \dfrac{\color{#FA7921}{9}}{\color{#3B87CD}{2x-6}} + \color{#3A9A38}{4} \\&= \dfrac{\color{#FA7921}{9}}{\color{#3B87CD}{2(x-3)}} + \color{#3A9A38}{4} \end{align}||
Voici deux exemples de résolution d'équation rationnelle.
-
Soit la fonction |f(x)=\dfrac{3}{x-4}+2.|
Détermine la valeur de |x| lorsque |f(x)=7.| ||\begin{align} f(x) &= \dfrac{3}{x-4}+2 \\7 &= \dfrac{3}{x-4}+2 \\5 &= \dfrac{3}{\color{#ec0000}{(x-4)}} \\5\color{#ec0000}{(x-4)} &= 3 \\5x-20 &= 3 \\ 5x &= 23 \\ x &= 4{,}6 \end{align}|| -
Soit la fonction |f(x)=\dfrac{6x+21}{2x+8}.|
Détermine la valeur de |x| lorsque |f(x)=3.|||\begin{align}f(x)&=\dfrac{6x+21}{2x+8}\\3 &=\dfrac{6x+21}{\color{#ec0000}{2x+8}}\\3\color{#ec0000}{(2x+8)}&=6x+21\\6x+24&=6x+21\\24 &\color{#ec0000}{=}21\quad\Rightarrow\ \text{Faux!}\end{align}||Comme on arrive à une égalité qui est toujours fausse, cela signifie qu'il n'y a aucune solution. La valeur |3| est celle de l’une des asymptotes.
Fonction exponentielle avec |a,| |b| et |c|
||f(x)=a(c)^{bx}||où
|y=0| correspond à l’équation de l’asymptote horizontale.
|a| correspond à la valeur initiale.
Fonction exponentielle avec |a,| |b,| |c,| |h| et |k|
||f(x)=a(c)^{b(x-h)}+k||où
|y=k| correspond à l’équation de l’asymptote horizontale.
|a+k| correspond à la valeur initiale.
Remarque : La plupart du temps, on utilise la forme canonique simplifiée. ||f(x)=a(c)^x +k||
-
Le paramètre |c| représente le facteur multiplicatif.
-
Le paramètre |b| représente le nombre de fois que le facteur multiplicatif est appliqué dans une période donnée.
Pour passer de la forme exponentielle à la forme logarithmique, on peut utiliser le schéma suivant.
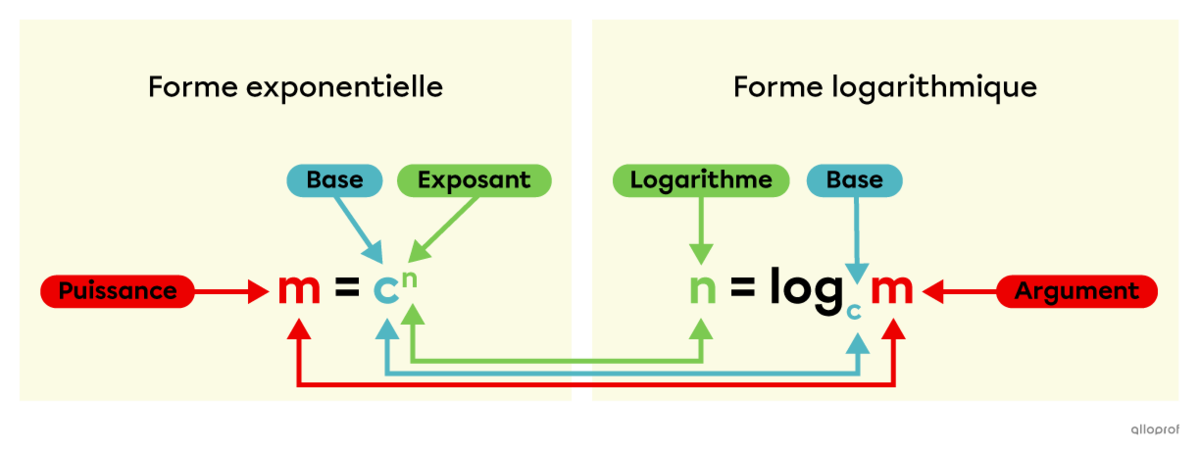
Exemple :||\color{#EC0000}{46}=\color{#51B6C2}3^{\color{#3A9A38}{2x}}\quad\Leftrightarrow \quad \color{#3A9A38}{2x}=\log_\color{#51B6C2}3\color{#EC0000}{46}||Voici deux exemples de résolution d’équations exponentielles.
Soit la fonction |f(x)=\dfrac{1}{8}(4)^x+5.|
-
Détermine la valeur de |x| lorsque |f(x)=13.|||\begin{gather}\begin{aligned}f(x)&=\dfrac{1}{8}(4)^x+5\\13&=\dfrac{1}{8}(4)^x+5\\8&=\dfrac{1}{8}(4)^x\\\color{#EC0000}{64}&=\color{#51B6C2}4^\color{#3A9A38}x\end{aligned}\\\Updownarrow\\\begin{aligned}\color{#3A9A38}x&=\log_{\color{#51B6C2}4}\color{#EC0000}{64}\\x&=3\end{aligned}\end{gather}||
-
Détermine la valeur de |x| lorsque |f(x)=2.|||\begin{gather}\begin{aligned}f(x)&=\dfrac{1}{8}(4)^x+5\\2&=\dfrac{1}{8}(4)^x+5\\-3&=\dfrac{1}{8}(4)^x\\\color{#EC0000}{-24}&=\color{#51B6C2}4^\color{#3A9A38}x\end{aligned}\\\Updownarrow\\\begin{aligned}\color{#3A9A38}x&=\log_{\color{#51B6C2}4}(\color{#EC0000}{-24})\end{aligned}\end{gather}||Puisque l’argument d’un logarithme ne peut pas être plus petit que |0,| il n’y a aucune solution.
Fonction logarithmique avec |a,| |b| et |c|
||f(x)=a\log_c({bx})||où
|x=0| correspond à l’équation de l’asymptote verticale.
Fonction logarithmique avec |a,| |b,| |c,| |h| et |k|
||f(x)=a\log_c\big({b(x-h})\big)+k||où
|x=h| correspond à l’équation de l’asymptote verticale.
Remarque : La plupart du temps, on utilise la forme canonique simplifiée. ||f(x)=\log_c\big({b(x-h})\big)||
Pour passer de l’écriture logarithmique à l’écriture exponentielle, on peut utiliser le schéma suivant.
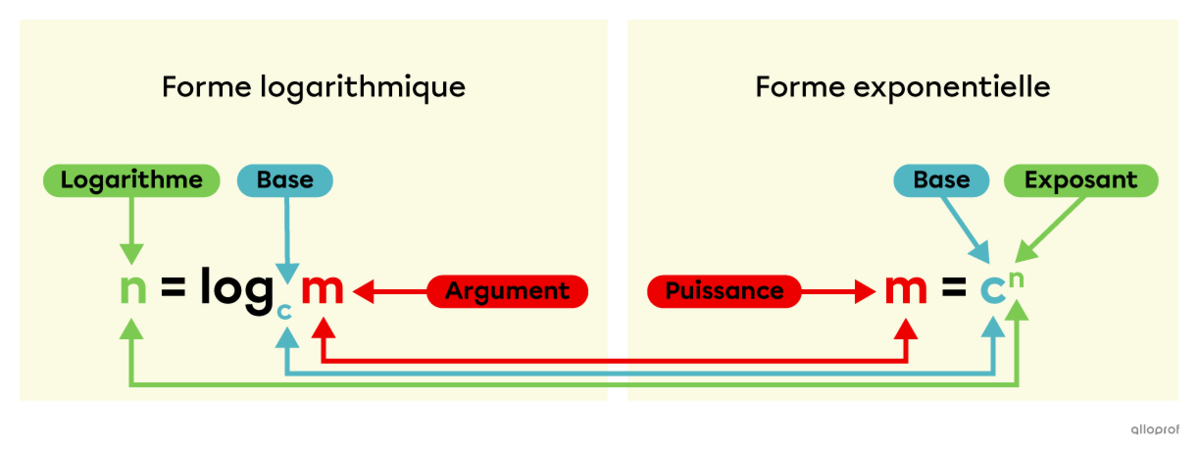
Exemple :||\color{#3A9A38}{10}=\log_\color{#51B6C2}2\color{#EC0000}x\quad \Leftrightarrow \quad \color{#EC0000}x=\color{#51B6C2}2^{\color{#3A9A38}{10}}||Le logarithme népérien (ou logarithme naturel) est un logarithme en base |e.| Le nombre |e| est un nombre décimal périodique et infini, et sa valeur est d'environ |2{,}718\ 28…|
||\ln x=\log_e x||où||e\approx 2{,}72||
Voici un exemple de résolution d’équation logarithmique.
Soit la fonction |f(x)=-\log_{\frac{3}{2}}\left(\dfrac{1}{6}(x+3)\right)-2.|
Détermine la valeur de |x| lorsque |f(x)=-3.|||\begin{gather}\begin{aligned}
f(x)&=-\log_{\frac{3}{2}}\left(\dfrac{1}{6}(x+3)\right)-2\\ -3&=-\log_{\frac{3}{2}}\left(\dfrac{1}{6}(x+3)\right)-2\\ -1&=-\log_{\frac{3}{2}}\left(\dfrac{1}{6}(x+3)\right)\\ \color{#3A9A38}1&=\log_{\color{#51B6C2}{\frac{3}{2}}}\left(\color{#EC0000}{\dfrac{1}{6}(x+3)}\right)
\end{aligned}\\\Updownarrow\\\begin{aligned}
\color{#EC0000}{\dfrac{1}{6}(x+3)}&=\left(\color{#51B6C2}{\frac{3}{2}}\right)^{\color{#3A9A38}1}\\ x+3&=9\\ x&=6\end{aligned}\end{gather}||